Erläuterungen
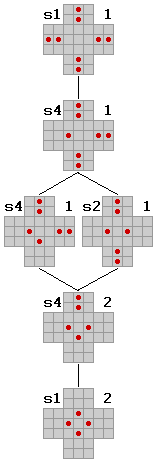
Die Bedeutung der einzelnen Tabellen und Ergebnisse soll hier anhand des
Beispielfelds genauer erläutert werden.
Patterns (Muster)
Die Patterns-Statistik gibt die Anzahl der verschiedenen Muster auf jeder
Ebene des Baums an, aufgeteilt in die verschiedenen Symmetrietypen. Der
Gesamtbaum (All) ist mit dem Normalbaum (Nrm) direkt korreliert, ein s4-Muster
in Nrm entspricht 4 Mustern in All. Entsprechend errechnet sich die All-Summe.
Dasselbe gilt für die Muster mit 0 möglichen Zügen.
| Patterns |
| Stones |
s1 |
s2 |
s4 |
s8 |
Nrm |
All |
| 8 |
1 |
0 |
0 |
0 |
1 |
1 |
| 7 |
0 |
0 |
1 |
0 |
1 |
4 |
| 6 |
0 |
1 |
1 |
0 |
2 |
6 |
| 5 |
0 |
0 |
1 |
0 |
1 |
4 |
| 4 |
1 |
0 |
0 |
0 |
1 |
1 |
| Sum |
2 |
1 |
3 |
0 |
6 |
16 |
| Patterns with 0 moves |
| Stones |
s1 |
s2 |
s4 |
s8 |
Nrm |
All |
EndWays |
EndWays |
| 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
1 |
0 |
0 |
0 |
1 |
1 |
2 |
24 |
| Sum |
1 |
0 |
0 |
0 |
1 |
1 |
2 |
24 |
Moves (Züge)
Ein Zug entspricht einer Verbindungslinie zwischen zwei Ebenen. Durch die
symmetrischen Zusammenfassungen existiert hier keine offensichtliche
Korrelation zwischen den beiden Bäumen.
| Moves |
| Stones |
s1 |
s2 |
s4 |
s8 |
Nrm |
s1 |
s2 |
s4 |
s8 |
All |
| 8 |
1 |
0 |
0 |
0 |
1 |
4 |
0 |
0 |
0 |
4 |
| 7 |
0 |
0 |
2 |
0 |
2 |
0 |
0 |
12 |
0 |
12 |
| 6 |
0 |
1 |
1 |
0 |
2 |
0 |
4 |
8 |
0 |
12 |
| 5 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
0 |
4 |
| 4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| Sum |
1 |
1 |
4 |
0 |
6 |
4 |
4 |
24 |
0 |
32 |
| Overview Nrm/All |
| Stones |
Patterns |
Pat0Moves |
Moves |
EndWays |
Patterns |
Pat0Moves |
Moves |
EndWays |
| 8 |
1 |
0 |
1 |
0 |
1 |
0 |
4 |
0 |
| 7 |
1 |
0 |
2 |
0 |
4 |
0 |
12 |
0 |
| 6 |
2 |
0 |
2 |
0 |
6 |
0 |
12 |
0 |
| 5 |
1 |
0 |
1 |
0 |
4 |
0 |
4 |
0 |
| 4 |
1 |
1 |
0 |
2 |
1 |
1 |
0 |
24 |
| Sum |
6 |
1 |
6 |
2 |
16 |
1 |
32 |
24 |
Patterns(Moves)
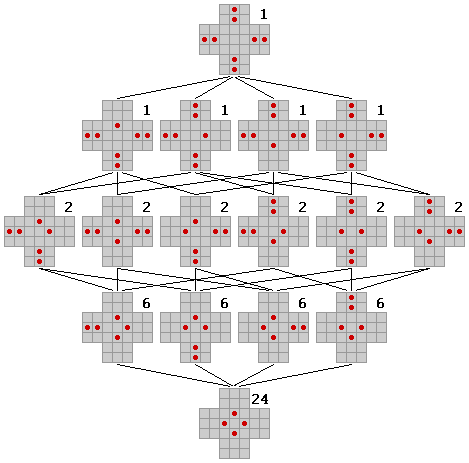
Diese Statistik gibt eine Aufstellung, wie viele Muster es mit einer
bestimmten Zahl von Zügen gibt. Die Zahl der Züge eines Musters
ist im jeweiligen Baum identisch mit der Anzahl der Verbindungslinien, die
von diesem Muster ausgehend in die nächste Ebene führen. Die
Summenzeile wiederholt die Gesamtzahl aller möglichen Züge aus der
Moves-Tabelle. 6 Muster mit 2 Zügen ergeben dabei 12 Züge, die in
die Summe 32 einfließen.
| Patterns(Moves) |
| Moves |
s1 |
s2 |
s4 |
s8 |
Nrm |
s1 |
s2 |
s4 |
s8 |
All |
| 0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
2 |
0 |
4 |
0 |
0 |
4 |
0 |
4 |
| 2 |
0 |
0 |
1 |
0 |
1 |
0 |
2 |
4 |
0 |
6 |
| 3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
4 |
| 4 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
| Sum |
1 |
1 |
4 |
0 |
6 |
4 |
4 |
24 |
0 |
32 |