Problemanalyse

Das Spielfeld besteht aus 33 Feldern mit binärer Stelleninformation (kein Stein - ein Stein). Das Spiel beginnt mit 32 Steinen und endet mit minimal einem Stein. Pro Zug wird exakt ein Stein entfernt. Es sind also maximal 31 Züge möglich, um ein Spielende zu erreichen. Zum Erreichen des Spielziels muss das Spielfeld in 31 Zügen in sein binäres Inverses überführt werden.

..111..
..111..
1111111
1110111
1111111
..111..
..111..
    

..111..
..101..
1110111
1111111
1111111
..111..
..111..
    

..000..
..000..
0000000
0000110
0000000
..000..
..000..
    

..000..
..000..
0000000
0001000
0000000
..000..
..000..
    

Beobachtung: Zu jedem Lösungsweg gibt es einen weiteren Lösungsweg, der das binäre Inverse des ersten Weges ist. Von links nach rechts überspringt eine 1 eine 1 und landet auf einer 0; von rechts nach links überspringt eine 0 eine 0 und landet auf einer 1. Durch eine Gesamtinvertierung wird dies umgekehrt, von rechts nach links findet sich nun ein weiterer Lösungsweg. Für die vollständige statistische Erfassung des Spiels hat diese Eigenschaft allerdings keine weitere Relevanz.

Beim Spiel handelt es sich um ein typisches Backtracking-Problem, es ist vollständig als Baumstruktur darstellbar. Zur Begriffsfestlegung bezeichne die Nummer der Ebene die Anzahl der Steine auf dem Feld. Ganz oben in Ebene 32 befindet sich die Wurzel mit dem Startzustand. Der Startzustand bietet 4 Zugmöglichkeiten, entsprechend befinden sich in Ebene 31 vier Feldzustände, auf die der Startzustand verzweigt. Jeder dieser 4 Zustände in Ebene 31 bietet seinerseits 3 Zugmöglichkeiten, in Ebene 30 befinden sich damit bereits 12 verschiedene Zustände, usw. Ein Endzustand ohne Zugmöglichkeiten ist ein Blatt ohne weitere Verzweigung.

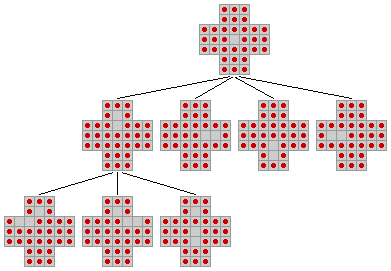
Wird der Baum rekursiv durchsucht (die übliche Vorgehensweise bei Backtracking-Problemen), so entspricht jedes Blatt einem Endzustand und damit einem Spielweg. Sowohl die Wege als auch die Muster sind damit vollständig statistisch erfassbar. Als Abschätzung sei angenommen, dass im Durchschnitt in jedem erreichbaren Feld 4 Züge möglich sind. Diese Zahl wird sehr wahrscheinlich zu klein sein, bietet jedoch eine Abschätzung für die untere Grenze. Weiterhin sei angenommen, dass sich die Endzustände auf die Züge 25 bis 31 gleichverteilen, im Schnitt also 28 Züge durchgeführt werden. Damit ergeben sich 4²⁸ = 2⁵⁶ Wege durch den Baum. Für eine vollständige Brute Force Rekursion sind dies Größenordnungen zu viel.

Vereinfachungen und Ansätze

Das Spielfeld und der Spielbaum weisen mehrere Eigenschaften auf, deren Ausnutzung die Komplexität des Problems erheblich reduziert.

Vernetzung

Mit 33 Feldpositionen sind maximal 2³³ Feldmuster möglich. Dies ist eine absolute obere Grenze, die oben erfolgte Darstellung der Baumwurzel weist darauf hin, dass bei weitem nicht alle möglichen Muster erreicht werden. Die Diskrepanz zwischen 2⁵⁶ Spielwegen als untere Abschätzung und 2³³ Feldmustern als obere Grenze deutet auf eine hochgradige Vernetzung oder Vermaschung des Baumes hin. Im offenen Baum kommt jedes Muster mehrfach vor. Der Baum kann so zusammengefasst werden, dass jedes Muster nur einmal vorkommt.

Die Vernetzung resultiert daher, dass voneinander unabhängige Züge in jeder beliebigen Reihenfolge ausgeführt werden können, aber trotzdem zum selben Ergebnis führen. Sind in den 4 Ecken des Feldes 4 Züge möglich, so ergeben sich daraus 4! = 24 Zugfolgen.

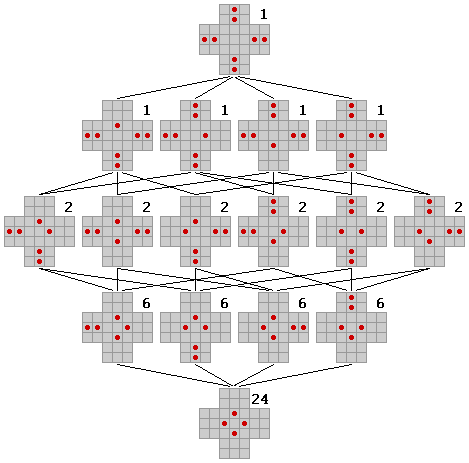
Jedes Feld kommt einmal im Baum vor und führt einen Zähler mit sich, der festhält, auf wie vielen verschiedenen Wegen dieses Feld erreicht wurde. In der Wurzel wird dieser Zähler mit 1, in allen anderen Feldern mit 0 initialisiert. Wird ein Feld erreicht, dann wird der Zähler des Quellfeldes zum Zähler des Zielfeldes addiert. Zum schnellen Vergleich, ob ein Muster bereits erreicht wurde, können alle Muster in einer Hashtabelle gespeichert werden, wobei sich der Hashkey aus dem Muster berechnet.

Symmetrie

Durch Drehung und Spiegelung können aus einem Feld bis zu 8 zueinander symmetrische Muster entstehen. Dabei treten 4 verschiedene Symmetriestufen auf.

Stufe	Beispiel	Anzahl Muster	Bezeichnung
Vollsymmetrie		1	s1
Halbsymmetrie		2	s2
Viertelsymmetrie		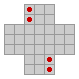4	s4
Asymmetrie		8	s8

Wird ein Feld in ein symmetrisches Äquivalent überführt, dann wird der gesamte Subbaum dieses Feldes auf entsprechende Weise umgeformt. Sowohl die Anzahl der Spielwege als auch die erreichbaren Felder bleiben bis auf die symmetrische Umformung identisch. Der Baum kann also weiter zusammengefasst werden, wenn ein symmetrisches Normal eingeführt wird. D.h., alle 8 Felder einer s8-Asymmetrie werden auf dasselbe Feld zurückgerechnet. Die weitere Rekursion wird mit diesem Feld vorgenommen.

 

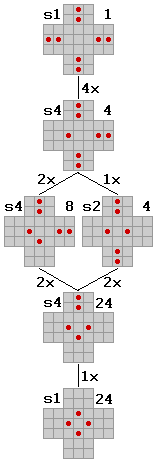
Die Ermittlung der Spielwege funktioniert weiterhin durch Addition, unabhängig von der Symmetrie der Baumwurzel. Die Muster kommen ihrer Symmetriestufe entsprechend oft im nicht normalisierten Baum vor, damit kann die Musterstatistik ermittelt werden. Dies hat jedoch die Vollsymmetrie der Wurzel, also des Startfeldes als Bedingung. In diesem Fall erhält man auch die Anzahl der Spielwege der nicht normalisierten Felder durch die Division der normalisierten Spielwege durch die Symmetriestufe.

Suchrichtung

Die rekursive Tiefensuche bereitet mehrere Probleme. Zum einen muss der gesamte Baum im Speicher gehalten werden, was auch normalisiert erhebliche Ressourcen beansprucht. Zum anderen bringt es keine Ersparnis bei der Suche, da die Vernetzung nicht ausgenutzt werden kann. Ganz im Gegenteil ist die additive Ermittlung der Spielwege nicht ohne weiteres möglich, da für jeden Weg die komplette Suche bis hinunter zu den Endmustern durchgeführt werden müsste. Andernfalls würde die Wegsumme in diesen Mustern nicht mehr stimmen.

Da eine Ebene ausschließlich von der unmittelbar darüberliegenden Ebene abhängig ist, kann statt der rekursiven Tiefensuche eine iterative Breitensuche durchgeführt werden. Die Suche wird mit dem Startfeld in Ebene 32 initialisiert, oder um beim Beispielbaum zu bleiben mit dem Startfeld in Ebene 8. Dieses Startfeld wird in eine Schleifentabelle eingetragen. Für jede Ebene n kann nun jedes Feld F aus der Schleifentabelle durchgerechnet werden, die Sprungergebnisse (die alle in Ebene n-1 liegen) werden in eine Suchtabelle eingetragen. Ist dies erfolgt, wird das Feld F statistisch verarbeitet und kann anschließend direkt gelöscht werden. Ist die Schleifentabelle leer, wird der Inhalt der Suchtabelle in die Schleifentabelle verschoben und die nächste Ebene n-2 berechnet. Dies wird solange durchgeführt bis keine Felder mehr vorhanden sind, da im Beispiel Ebene 4 keine Nachfolger in Ebene 3 hat.

Dies hat die Vorteile:

• Rechenzeit
  • Additive Ermittlung der Spielwege
  • Iterative Schleifen statt rekursive Funktionsaufrufe
  • Jedes Feld wird genau einmal auf Sprungmöglichkeiten durchsucht und statistisch erfasst.
• Speicher
  • Es werden maximal 2 Ebenen im Speicher gehalten, durch die sofortige Löschung der verarbeiteten Felder auch nur teilweise.